Well, I can't answer the questions about self-feedback yet. I haven't started doing any serious testing of self-feedback, but when I do, I'll definitely investigate these issues and see if I can track down the cause. I can post a lot of info about other aspects of the operator unit however. They should be an interesting read for someone. I've also finished my testing on the phase generator and accumulator. I'll write up my findings in those areas once I've got some time free. Until then, here's the OPN operator unit in a nutshell.
The core of the operator unit is the process involved in evaluating a single operator. That process involves taking a 10-bit output from the envelope generator, a 10-bit output from the phase generator, a 10-bit phase modulation input (generated by the operator unit itself from either self-feedback or modulation by another operator), and producing a single 14-bit result, which is then either output to the accumulator or used to modulate another operator. The steps involved in generating this 14-bit output are IMO the most poorly expressed and documented parts of the MAME core, and you'd be hard pressed to figure out what was going on by looking at the MAME implementation alone.
There's one very important thing to note before I say anything more about the operator unit. There's a very big lie in all of the OPN documentation. You will read time and time again that the envelope generator has the power to attenuate the output by between 0db and 96db. This is incorrect. In fact, the envelope generator can only attenuate the output by 0db to 48db. This doesn't change anything about how you implement the envelope generator itself, but for every table you see in any documentation that discusses decibels, you need to divide every value by 2 to get the real attenuation values. TL is actually 0-48db. SL is actually 0-12db (or 48db when all set), and the 10-bit output of the envelope generator itself is of course 0 to 48db. There wouldn't be much point in giving the envelope generator a 96db range. The output of the OPN operator unit is only 14-bit, and lacks the resolution required in order to represent numbers over around 40db attenuation anyway. Anything past that point just outputs 0, so they couldn't have implemented a 96db effective range without a significant increase in the precision of the operator unit.
On paper, the calculations the operator unit performs are simple. The operator unit simply has to calculate the sine value for the phase, and attenuate it by the output from the envelope generator. That's it. You could implement the operator unit like this:
Code: Select all
//attenuationBitCount = 10
//phaseBitCount = 10
//operatorOutBitCount = 14
//phase = the output from the phase generator
//attenuation = the output from the envelope generator
//Calculate the sine value
double phaseNormalized = ((double)phase / ((1 << phaseBitCount) - 1))
double sinResult = sin(phaseNormalized * M_PI * 2);
//Convert the attenuation to a linear representation of power
double attenuationIndividualBitWeighting = 48.0 / (1 << attenuationBitCount);
double attenuationInBels = (((double)attenuation * attenuationIndividualBitWeighting) / 10.0);
double powerLinear = pow(10.0, -attenuationInBels);
//Attenuate the result
double resultNormalized = sinResult * powerLinear;
//Calculate the 14-bit operator output
unsigned int maxOperatorOutput = ((1 << (operatorOutBitCount - 1)) - 1);
int result = (int)(resultNormalized * maxOperatorOutput);
This was actually my first implementation. It works, and if the YM2612 was a "perfect" device, this would actually be a very accurate implementation. In reality, Yamaha had to actually build the operator unit as a physical device, and they had to do it as cheaply and efficiently as possible, within the boundaries of what was possible with the technology of the time. The end-result is that the operator unit is not as precise as the calculation which is performed above. I doubt you'll hear any audible difference, but if you want to build an accurate emulator, it is possible to perfectly emulate the operator unit calculations performed by the YM2612, but the implementation is a little more complex than the algorithm I've just presented.
I've done a lot of analysis and testing, and I've figured out what I believe are the exact steps the real operator unit performs. I can guarantee if you follow the information I'm about to show, you will be able to create a 100% binary exact implementation of the YM2612 operator unit. I've implemented all of this in my YM2612 core, and it works a treat. It is worth noting that MAME already gets a 100% accurate output for this area, though the implementation is a little hard to understand.
I found the easiest way to document the core of the operator unit was using a diagram. They say a picture says a thousand words, so hopefully this will save me some typing:
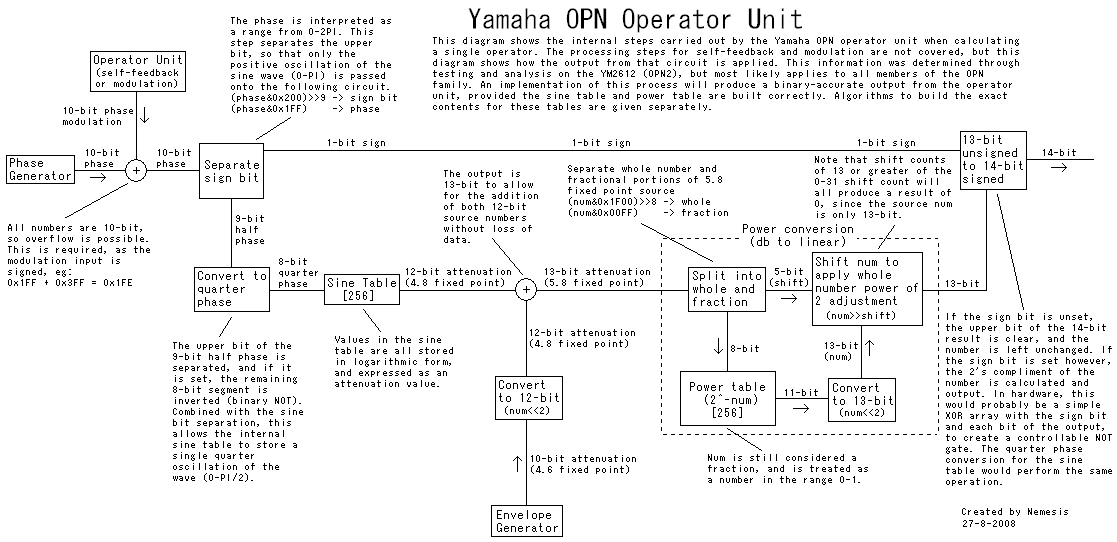
Here's my (heavily commented) algorithm to build the perfect contents for the sine table:
Code: Select all
//sinTableBitCount = 8
//attenuationFixedBitCount = 8
for(unsigned int i = 0; i < (1 << sinTableBitCount); ++i)
{
//Calculate the normalized phase value for the input into the sine table. Note
//that this is calculated as a normalized result from 0.0-1.0 where 0 is not
//reached, because the phase is calculated as if it was a 9-bit index with the
//LSB fixed to 1. This was done so that the sine table would be more accurate
//when it was "mirrored" to create the negative oscillation of the wave. It's
//also convenient we don't have to worry about a phase of 0, because 0 is an
//invalid input for a log function, which we need to use below.
double phaseNormalized = ((double)((i << 1) + 1) / (1 << (sinTableBitCount + 1)));
//Calculate the pure sine value for the input. Note that we only build a sine
//table for a quarter of the full oscillation (0-PI/2), since the upper two bits
//of the full phase are extracted by the external circuit.
double sinResultNormalized = sin(phaseNormalized * (M_PI / 2));
//Convert the sine result from a linear representation of volume, to a
//logarithmic representation of attenuation. The YM2612 stores values in the sine
//table in this form because logarithms simplify multiplication down to addition,
//and this allowed them to attenuate the sine result by the envelope generator
//output simply by adding the two numbers together.
double sinResultAsAttenuation = -log(sinResultNormalized) / log(2.0);
//The division by log(2) is required because the log function is base 10, but the
//YM2612 uses a base 2 logarithmic value. Dividing the base 10 log result by
//log10(2) will convert the result to a base 2 logarithmic value, which can then
//be converted back to a linear value by a pow2 function. In other words:
//2^(log10(x)/log10(2)) = 2^log2(x) = x
//If there was a native log2() function provided we could use that instead.
//Convert the attenuation value to a rounded 12-bit result in 4.8 fixed point
//format.
unsigned int sinResult = (unsigned int)((sinResultAsAttenuation * (1 << attenuationFixedBitCount)) + 0.5);
//Write the result to the table
sinTable[i] = sinResult;
}
And here's my algorithm to build the perfect contents for the power table:
Code: Select all
//powTableBitCount = 8
//powTableOutputBitCount = 11
for(unsigned int i = 0; i < (1 << powTableBitCount); ++i)
{
//Normalize the current index to the range 0.0-1.0. Note that in this case, 0.0
//is a value which is never actually reached, since we start from i+1. They only
//did this to keep the result to an 11-bit output. It probably would have been
//better to simply subtract 1 from every final number and have 1.0 as the input
//limit instead when building the table, so an input of 0 would output 0x7FF,
//but they didn't.
double entryNormalized = (double)(i + 1) / (double)(1 << powTableBitCount);
//Calculate 2^-entryNormalized
double resultNormalized = pow(2, -entryNormalized);
//Convert the normalized result to an 11-bit rounded result
unsigned int result = (unsigned int)((resultNormalized * (1 << powTableOutputBitCount)) + 0.5);
//Write the result to the table
powTable[i] = result;
}
I'd also suggest you wrap the entire power conversion into a function like this:
Code: Select all
unsigned int YM2612::InversePow2(unsigned int num) const
{
unsigned int shiftCount = num >> powTableBitCount;
unsigned int tableIndex = num & ((1 << powTableBitCount) - 1);
unsigned int tableEntry = powTable[tableIndex];
unsigned int outputShifted = (tableEntry << 2) >> shiftCount;
return outputShifted;
}
A quick note about fixed point, in case you've never encountered that term before. What "fixed point" means is that a number is an integer value, but one or more of the bits in the number are treated as if they were after the decimal place, so you could represent non-whole numbers like 3.6 or 1.5. In the case of a 4.8 fixed point number, the upper 4 bits are used to represent the whole number portion, while the lower 8 bits are used to represent the "fractional" portion below the decimal place, meaning 1.5 would be represented by 0x180 for example. You'll see that the operator unit uses fixed point math when handling attenuation values.
Everything you should need to implement a perfect operator unit is shown above. What I'm going to do now is simply talk about how the actual implementation created by Yamaha relates to the "perfect" algorithm shown right at the start, so you can understand why the Yamaha implmentation works. You'll need to be clear on logarithms first of all. I find it easiest to think of a logarithm as the "reverse" of a power function, so:
10^log10(num)=log10(10^num)=num
The envelope generator output is represented in decibels. Decibels are a 10th of a "bel", so a value of 48 decibels is 4.8 bels. Bels are a value on the base 10 logarithmic scale. This means in order to convert back to a linear value, we would need to use a pow10 function, or 10^num, where num is a base 10 number representing a value in bels. In the case of attenuation, you could calculate 10^-num to get a normalized representation of the attenuation in the linear scale. In the first algorithm I presented, this is exactly what we did. The 10-bit attenuation output from the envelope generator was scaled to a floating point value between 0 and 4.8, and converted to a linear normalized result.
Yamaha don't do this in the YM2612. Instead, they use a useful property of logarithms to reduce the work the operator unit has to do. Logarithms reduce multiplication down to addition. As you'll find right near the top of the wiki article, log(x * y) = logx + logy. Yamaha took advantage of this fact when designing the OPN operator unit. Rather than convert the attenuation from the envelope generator into a linear scale and multiply it with the output from the sine table, they converted the sine table itself to return values which are also a logarithmic representation of attenuation. This allowed them to simply add the two numbers together, then convert the whole thing back to a linear scale to get the final output, doing away with the need for multiplication. This is the reason the sine table in the YM2612 is built in a non-standard way, it's the reason the power conversion happens after the sine value is attenuated by the envelope generator output, and it's the reason the attenuation from the envelope generator and the output from the sine table are simply added together.
There's one remaining quirk about the implementation which needs explanation, and that's all about bases. In the algorithm I presented at the start, we convert the envelope generator output to an expression of attenuation in bels, then use a base 10 power function to convert from bels, which is a base 10 logarithmic scale, to a linear value. You'll see the Yamaha implementation uses a base 2 power function to convert back to a linear value however. That's not a problem for the sine table, as you'll see in the comments for building the sine table that we (effectively) use a base 2 log function to build the table, so the base 2 power function is the valid conversion to turn those back to linear values. What about the envelope generator output though? We talk about the attenuation of the envelope generator in decibels, and doesn't that require a base 10 power function to convert back to a linear scale?
First of all, here's the weighting table I gave previously for the 10-bit envelope generator output:
Code: Select all
EG attenuation output bit weighting = 96 / 2^10
---------------------------------------------------------------------------------
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|-------------------------------------------------------------------------------|
| 48 | 24 | 12 | 6 | 3 | 1.5 | 0.75 | 0.375 | 0.1875|0.09375|
---------------------------------------------------------------------------------
Given that the official documentation is incorrect, and that the output of the envelope generator is 0-48db, this is the actual weighting of each bit of the output:
Code: Select all
EG attenuation output bit weighting = 48 / 2^10
----------------------------------------------------------------------------------
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|--------------------------------------------------------------------------------|
| 24 | 12 | 6 | 3 | 1.5 | 0.75 | 0.375 | 0.1875|0.09375|0.046875|
----------------------------------------------------------------------------------
You can see from the diagram above that I indicate this 10-bit output is also actually a 4.6 fixed point value, like so:
Code: Select all
|------Whole number portion-----|---------------Fractional portion---------------|
----------------------------------------------------------------------------------
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|--------------------------------------------------------------------------------|
| 24 | 12 | 6 | 3 | 1.5 | 0.75 | 0.375 | 0.1875|0.09375|0.046875|
----------------------------------------------------------------------------------
First of all, you'll note that these numbers are not in base 10 at all. Bit 6, which is the first "whole number" bit of the output, actually has a reported weighting of 3db. If this was a base 10 number, 3db would be represented by a whole number value of 0x03, not 0x01, and 24db would be represented by a whole number value of 0x18, whereas here it's 0x08.
To understand what's going on here, have a look at the code to build the sine table. We need to calculate a log2 value, but there's only a log10 function available. We can in fact convert a log10 value into a log2 value using a useful identity however. As presented in the comments, that identity as it applies to this case is as follows:
2^(log10(x)/log10(2))=2^log2(x)=x
In more general terms, if you divide the result of logx(num) value by logx(y), where x and y are two arbitrary bases, you convert bases, giving you the same result as logy(num).
What that means is that if we wanted to convert from base 10 logarithmic values, that being the attenuation in bels in this case, into base 2 logarithmic values, we would have to divide the base 10 logarithmic value by log10(2). So, what is the value of log10(2)? Well, it's approximately 0.30103. That's fairly close to 0.3. The guys at Yamaha decided it was close enough. First of all, let's convert our attenuation values from decibels to bels, by simply dividing all the numbers by 10:
Code: Select all
|------Whole number portion-----|----------------Fractional portion----------------|
------------------------------------------------------------------------------------
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|----------------------------------------------------------------------------------|
| 2.4 | 1.2 | 0.6 | 0.3 | 0.15 | 0.075 | 0.0375|0.01875|0.009375|0.0046875|
------------------------------------------------------------------------------------
Now look what happens when we divide all those numbers in our weighting table by 0.3:
Code: Select all
|------Whole number portion-----|---------------Fractional portion---------------|
----------------------------------------------------------------------------------
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|--------------------------------------------------------------------------------|
| 8 | 4 | 2 | 1 | 0.5 | 0.25 | 0.125 | 0.0625|0.03125|0.015625|
----------------------------------------------------------------------------------
Now we see what we've actually got is straight values in powers of 2. This shows the output from the envelope generator is in fact a base 2 logarithmic expression of attenuation, and we can see from the table above it is in fact in 4.6 fixed point form, so we just need to convert it to 4.8 fixed point form, and it's ready to be combined with the output from the sine table.
And I think that's everything there is to know about how an operator is calculated. The only other parts of the operator unit which remain relate to how the phase modulation input is calculated for self-feedback and modulation.
